Actionscript:
-
[SWF(width = 600, height = 600)]
-
var a:Number = 0.02;
-
var b:Number = .9998;
-
-
var xn1:Number = 5;
-
var yn1:Number = 0;
-
var xn:Number, yn:Number;
-
-
var scale:Number = 10;
-
var iterations:Number = 20000;
-
-
function f(x:Number):Number{
-
var x2:Number = x * x;
-
return a * x + (2 * (1 - a) * x2) / (1 + x2);
-
}
-
-
var canvas:BitmapData = Bitmap(addChild(new Bitmap(new BitmapData(600,600,false,0xEFEFEF)))).bitmapData;
-
-
addEventListener(Event.ENTER_FRAME, onLoop);
-
function onLoop(evt:Event):void {
-
-
canvas.fillRect(canvas.rect, 0xEFEFEF);
-
a = mouseY / 1000;
-
xn1 = mouseX / 30;
-
yn1 = 0;
-
for (var i:int = 0; i<iterations; i++){
-
xn = xn1;
-
yn = yn1;
-
-
xn1 = b * yn + f(xn);
-
yn1 = -xn + f(xn1);
-
canvas.setPixel( 280 + xn1 * scale, 300 + yn1 * scale, 0x000000);
-
}
-
}
Notice the setup for this is very similar to yesterdays flames attractor post.
Back in october of last year I stumbled upon the excellent subblue website by Tom Beddard. I was REALLY impressed by a blog post about Gumowski / Mira patterns. If you haven't seen it you should go take a look.
I'd never heard of Gumowski / Mira patterns before and made a mental note to go and try to read about them and maybe find an equation to port to actionscript or processing. Anyway, a few days ago I decided to go ahead and look up the math and... this is the result.
I got equation over at mathworld...
For simplicity I intentionally made the actionscript code look as much like the mathworld equation as possible. Using f for my function name and using xn1, yn1 etc... There are a few speed optimizations that could be made but I wanted this snippet to be very readable.
Here are a few examples of what this code will generate:

Actionscript:
-
[SWF(width = 600, height = 600)]
-
var a:Number = 0.02;
-
-
var xn:Object = new Object();
-
-
var scale:Number = 20;
-
var iterations:Number = 10000;
-
-
var canvas:BitmapData = Bitmap(addChild(new Bitmap(new BitmapData(600,600,false,0xEFEFEF)))).bitmapData;
-
-
addEventListener(Event.ENTER_FRAME, onLoop);
-
function onLoop(evt:Event):void {
-
-
canvas.fillRect(canvas.rect, 0xEFEFEF);
-
a = mouseX / 100;
-
-
// equations from here: http://www.discretedynamics.net/Attractors/Flames.htm
-
// i used object syntax so that I could really reflect the math notation, changing these to
-
// 3 variables will significantly improve performance:
-
xn["n-1"] = mouseX / 200;
-
xn["n"] = mouseY / 200;
-
xn["n+1"] = 0;
-
-
for (var i:int = 0; i<iterations; i++){
-
-
xn["n+1"] = ((a * xn["n"]) / (1 + (xn["n-1"] * xn["n-1"]))) - ((xn["n-1"]) / (1 + (xn["n"] * xn["n"])));
-
-
canvas.setPixel( 280 + xn["n-1"] * scale, 300 + xn["n"] * scale, 0x000000);
-
-
xn["n-1"] = xn["n"];
-
xn["n"] = xn["n+1"];
-
}
-
}
This is an attractor that vaguely resembles flames, I wrote this code so that it would be very similar to the math notation to help anyone who wonders how to go from notation to code. You could replace the Object syntax with 3 separate variables for increased performance.
See the equation here:
http://www.discretedynamics.net/Attractors/Flames.htm
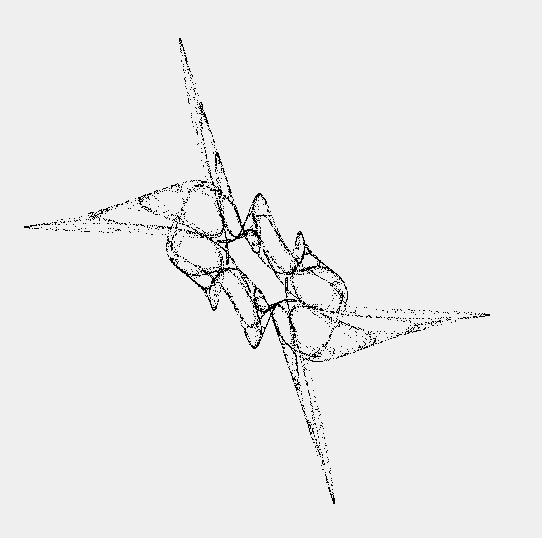
This snippet will create something that looks like this and is reactive to the mouse location
Actionscript:
-
[SWF(backgroundColor=0x000000, frameRate=30)]
-
-
var elements:Array = new Array();
-
for (var i:int = 0; i<200; i++){
-
var c:MovieClip= MovieClip(addChild(new MovieClip()));
-
c.x = Math.random()*(stage.stageWidth + 100) - 50;
-
c.y = Math.random()*stage.stageHeight;
-
with(c.graphics) lineStyle(2, 0xFFFFFF,3), drawCircle(0,0,2 + c.y / 20);
-
c.startX = c.x;
-
elements.push(c);
-
}
-
-
var offset:Number = 0;
-
var t:Number = 0;
-
-
addEventListener(Event.ENTER_FRAME, onLoop);
-
function onLoop(evt:Event):void {
-
t+=.1;
-
offset = 200 * Math.cos(t);
-
for (var i:int = 0; i<elements.length; i++){
-
elements[i].x = elements[i].startX + offset / ((stage.stageWidth - elements[i].y) / 80);
-
}
-
}
I wrote this snippet originally to automatically add parallax motion to a bunch of quick drawings I did within the flash IDE. Each movieClip in the elements array is moved from left to right based on it's y position. Clips with a higher y value will oscillate more from left to right than clips with lower y values.
Here is the original drawing I used this on.
And here is what the above snippet will create.
Posted in motion | Tagged actionscript, flash |
Actionscript:
-
// line thickness, line color, start point, end point, divisor, callback
-
function animateLineTo( thick:Number, col:uint, sp:Point, ep:Point, div:Number=4, callback:Function=null):void {
-
var s:Shape = Shape(addChild(new Shape()));
-
var ap:Point = sp.clone();
-
div = Math.max(2, div);
-
setTimeout(runLineAnimation, 1000/stage.frameRate, s.graphics , thick , col , sp , ep , ap, div, callback);
-
}
-
-
function runLineAnimation(g:Graphics , thick:Number, col:uint, sp:Point, ep:Point, ap:Point, div:Number, callback:Function):void {
-
ap.x += (ep.x - ap.x) / div;
-
ap.y += (ep.y - ap.y) / div;
-
with(g){
-
clear();
-
lineStyle(thick, col);
-
moveTo(sp.x, sp.y);
-
lineTo(ap.x, ap.y);
-
}
-
if (Math.abs(ap.x - ep.x) <1 && Math.abs(ap.y- ep.y) <1){
-
// done
-
if (callback!=null){
-
callback();
-
}
-
}else{
-
setTimeout(runLineAnimation, 1000/stage.frameRate, g , thick , col , sp , ep , ap, div, callback);
-
}
-
}
-
//
-
// test out the animateLineTo function:
-
//
-
var a:Point = new Point(100,100);
-
var b:Point = new Point(150, 200);
-
var c:Point = new Point(300, 190);
-
var d:Point = new Point(280, 90)
-
-
animateLineTo(0, 0xFF0000, a, b, 4, line2);
-
-
function line2():void{
-
animateLineTo(0, 0xFF0000, b, c, 4, line3);
-
}
-
-
function line3():void{
-
animateLineTo(0, 0xFF0000, c, d, 4, line4);
-
}
-
-
function line4():void{
-
animateLineTo(0, 0xFF0000, d, a, 4);
-
}
The above demos a function called animateLineTo() that will draw a line using zeno's paradox.
There are a couple weird/interesting tricks going on here. I'm using setTimeout() over and over rathaer than using setInterval(). This makes it so I don't need to store an interval id. I'm also using a delay of 1000/stage.frameRate, this attempts to cause the setTimeout() to run at the same frequency as an enter frame would. This is important because having a setTimeout()/setInterval() that is doing animation and attempting to run more frequently than the framerate can cause problems and is a waste of cpu power.
This snippet was spurned by a student question about how to animate a Graphics.lineTo() from point A to point B. Here is the original snippet, which is easier to read and more bare bones:
Actionscript:
-
var p0:Point = new Point(100,100);
-
var p1:Point = new Point(400,200);
-
var dp:Point = new Point(p0.x,p0.y);
-
-
var s:Sprite = Sprite(addChild(new Sprite()));
-
-
addEventListener(Event.ENTER_FRAME, onLoop);
-
function onLoop(evt:Event):void {
-
s.graphics.clear()
-
s.graphics.lineStyle(0,0x000000);
-
s.graphics.moveTo(p0.x, p0.y);
-
s.graphics.lineTo(dp.x, dp.y);
-
dp.x += (p1.x - dp.x) / 4;
-
dp.y += (p1.y - dp.y) / 4;
-
}
Posted in motion | Tagged actionscript, flash |

