Actionscript:
-
var canvas:BitmapData = new BitmapData(400,400,false, 0x000000);
-
addChild(new Bitmap(canvas));
-
-
var p0:Sprite = dot(100, 100);
-
var p1:Sprite = dot(120, 180);
-
var p2:Sprite = dot(220, 180);
-
var p3:Sprite = dot(250, 250);
-
-
addEventListener(Event.ENTER_FRAME, onLoop);
-
function onLoop(evt:Event):void {
-
canvas.lock();
-
canvas.fillRect(canvas.rect, 0x000000);
-
-
curve(p0, p1, p2, p3);
-
canvas.unlock();
-
}
-
-
-
// all math from http://en.wikipedia.org/wiki/Cubic_Hermite_spline
-
function curve(p0:Sprite, p1:Sprite, p2:Sprite, p3:Sprite, rez:Number=.02):void{
-
var px:Number = 0;
-
var py:Number = 0;
-
var m0:Point = tangent(p1, p0);
-
var m1:Point = tangent(p2, p0);
-
var m2:Point = tangent(p3, p1);
-
var m3:Point = tangent(p3, p2);
-
-
for (var t:Number = 0; t <1; t+=rez){
-
var t_2:Number = t * t;
-
var _1_t:Number = 1 - t;
-
var _2t:Number = 2 * t;
-
-
var h00:Number = (1 + _2t) * (_1_t) * (_1_t);
-
var h10:Number = t * (_1_t) * (_1_t);
-
var h01:Number = t_2 * (3 - _2t);
-
var h11:Number = t_2 * (t - 1);
-
-
px = h00 * p0.x + h10 * m0.x + h01 * p1.x + h11 * m1.x;
-
py = h00 * p0.y + h10 * m0.y + h01 * p1.y + h11 * m1.y;
-
canvas.setPixel(px, py, 0xFFFFFF);
-
-
px = h00 * p1.x + h10 * m1.x + h01 * p2.x + h11 * m2.x;
-
py = h00 * p1.y + h10 * m1.y + h01 * p2.y + h11 * m2.y;
-
canvas.setPixel(px, py, 0xFFFFFF);
-
-
px = h00 * p2.x + h10 * m2.x + h01 * p3.x + h11 * m3.x;
-
py = h00 * p2.y + h10 * m2.y + h01 * p3.y + h11 * m3.y;
-
canvas.setPixel(px, py, 0xFFFFFF);
-
}
-
}
-
-
function tangent(pk1:Sprite, pk_1:Sprite){
-
return new Point((pk1.x - pk_1.x) / 2, (pk1.y - pk_1.y) / 2);
-
}
-
-
// draggable dot
-
function dot(xp:Number, yp:Number, col:uint = 0x507399, rad:Number=5):Sprite {
-
var s:Sprite = Sprite(addChild(new Sprite));
-
s.x = xp;
-
s.y = yp;
-
with(s.graphics) beginFill(col), drawCircle(0,0,rad);
-
s.buttonMode = true;
-
s.addEventListener(MouseEvent.MOUSE_DOWN, onDrag);
-
return s;
-
}
-
function onDrag(evt:MouseEvent):void {
-
evt.currentTarget.startDrag()
-
}
-
stage.addEventListener(MouseEvent.MOUSE_UP, onUp);
-
function onUp(evt:MouseEvent):void{
-
stopDrag();
-
}
This is snippet draws a Catmull-Rom spline based on 4 control points. A nice feature of Catmull-Rom splines is that they always pass through each of their control points.
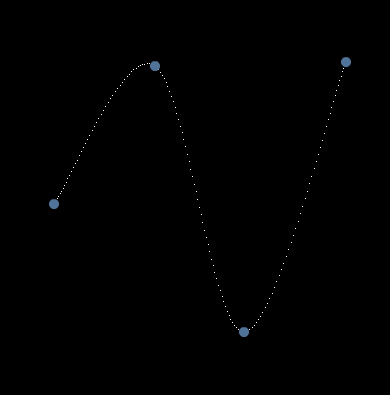
I first learned about Catmull-Rom splines somewhere in the processing forums.
I got all my info for this snippet from this wikipedia page.
There is a good deal of room for optimization here... I may post an optimized version in the future.
4 Comments
I can’t thank you enough. Any idea why the tangent equations on wikipedia were completely different?
no problem, glad this post helped you. whenever I wrote this post I used the code from wikipedia to write it, so I assume someone must have changed the wikipedia post if its different now.
Is there a way to draw solid lines between the points?
Thanks man - easiest spline code example. Ported this to Lua in 3D, works great.
One Trackback
[...] Quadratic Bezier Curve Bresenham line Bresenham Circle Catmull-Rom Spline [...]